強度計算
- トップ
- 強度計算
CAE解析,強度計算,設計計算,騒音・振動の測定と対策,ねじ締結部の設計,ボルト破断対策 のご相談は,ここ(トップページ)をクリックしてください。
強度計算の方法
一般的に行われている強度計算は「材料を塑性変形させない。」との発想で次式が成立すれば「強度は十分」と判断しています。安全率SFは 2 くらいでしょうか。

計算される応力σは,材料力学の範ちゅうで求まる応力で次式で計算されています。また,有限要素法で応力を求める場合はミゼス相当応力が使われます。

応力集中係数αを考慮しないと,手計算と有限要素法で大きな違いが生じます。有限要素法では応力集中が反映された応力を出力するので,手計算の場合より数倍大きな値となります。有限要素法を使った場合,安全側の強度判断となり,この結果を反映して設計すると多くの場合寸法が大きくなって不経済な設計となります。
疲労強度計算
繰返し荷重が作用する場合,下表に示すアンウィンによる安全率を用いた強度計算が広く行われています。この表は多くの文献に引用されていて,皆さんも見たことがあると思います。
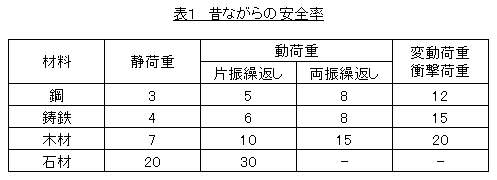
(2)ないし(3)式で応力σを求め,次式が成立すれば強度があると判断するものです。ただし,応力集中は考慮しません。α=1 です。

上式のσcは基準強さで,引張強さを用いることが多いです。
上記安全率は経験的に定められたようで,根拠を示す文献は見当たりません。この安全率で設計して,多くの場合疲労破壊に至らないので問題なさそうですが少し大雑把です。日本機械学会の便覧1)にはこの方法は記述されていませんし,機械を設計してそれを納めた顧客が「安全率の根拠を教えてください。」と言ったときに「アンウィンさんに聞いてください」とは言えないでしょう。
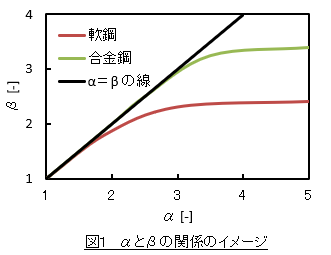
しかし,表1の値は的を得てます。下図は応力集中係数αと切欠係数βの関係です2)。文献の図をそのまま載せるわけにはいかなかったので,図を見て書き直しました。この図は,機械学会の文献など多くの設計解説書に引用されています。
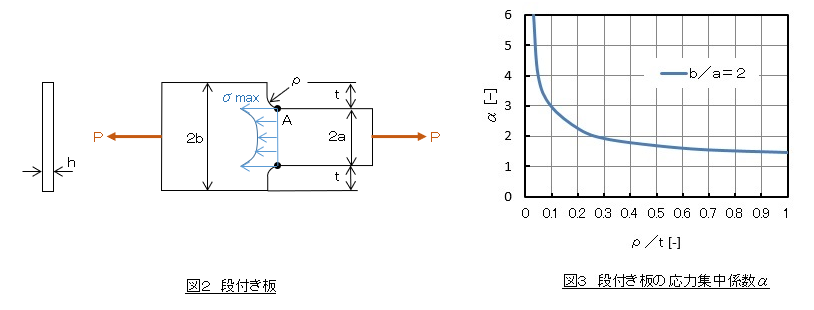
応力集中係数αは1から無限大の値をとります。例えば段付き板の応力集中係数3)を下図に示します。角の曲率半径ρがゼロに近づくとαは無限大になります。
図1を見ると応力集中係数αが大きくなったときの切欠係数βは約 3 程度にとどまります。この点に注目してください。
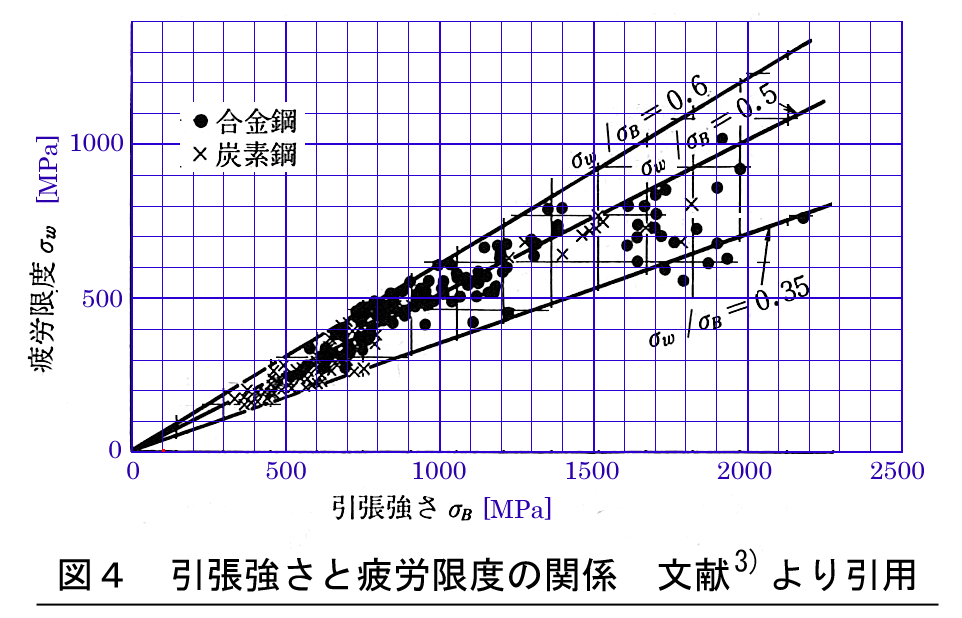
材料の疲労強度を求めましょう。鉄鋼材料の場合,無限回の繰返し荷重に耐える応力振幅が存在しこれを「疲労限度」と呼びます。アルミニウム材やステンレス鋼は無限回の繰返し荷重に耐える応力振幅がないので,107回程度の時間寿命を疲労強度とすることが多いです。このサイトでは,両者を合わせて疲労強度と呼ぶことにします。疲労強度は引張強さと比例関係にあり,図4に示すように引張強さの0.35倍が疲労強度(応力振幅)となります。
では応力集中と疲労を考慮したら材料強度がどのくらいになるか計算しましょう。応力集中で強度は1/3に,繰返し荷重で強度は0.35倍になります。両者をかけると次式となります。
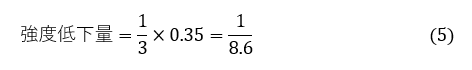
強度は1/8.6 倍となります。表1の鋼,両振繰返しの値 8 にほぼ一致します。以上のように表1の安全率は使っていて問題ないように思われます。
現在の強度計算
残念ながら上述した方法は「昔ながらの方法」と言わざるを得ません。例えば切欠係数 β が 3 より小さな場合は,この方法による設計では過剰な強度を持つことになりますし,疲労強度と引張強さの比を0.35としましたが,0.5でいいかもしれません。そして,図5に示すように,自重などによって変化しない応力成分(平均応力)がある場合,平均応力がゼロの場合(完全両振荷重)より小さな応力振幅で疲労破壊に至ります。これらの要因を個別に考慮するのが現在のやり方です。
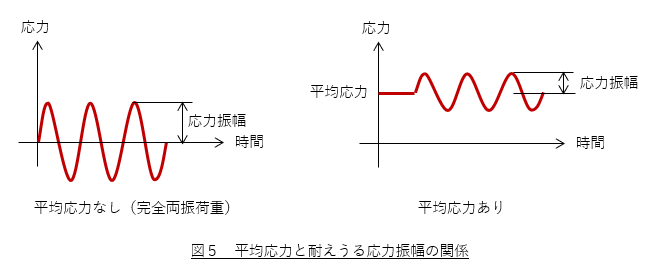
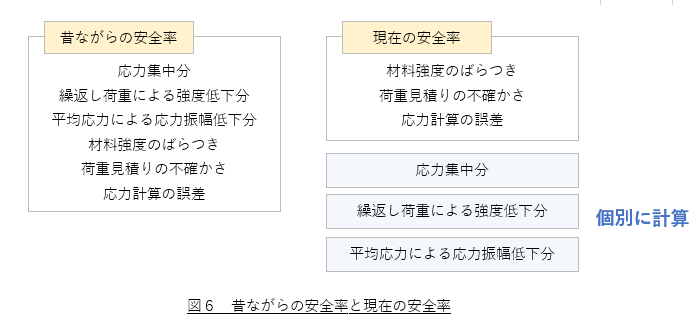
図6に示すように,昔ながらの方法は安全率にいろいろな要因を入れていました。しかし現在は,わかる要因は安全率の外に出して,不測な要因に対してだけ安全率を設定しようという考え方をしています。
機械学会の便覧では次式が提案されています1)。

fmとfsの積は,実機状態で十分な疲労試験ができ,過去の実績がある場合で1.2 程度の値をとることができるのですが,そのような環境は稀なので 2 以上の値とするのが無難です。
平均応力による応力振幅の低下は,図7に示した修正グッドマン線図によって疲労破壊の有無を予測します。
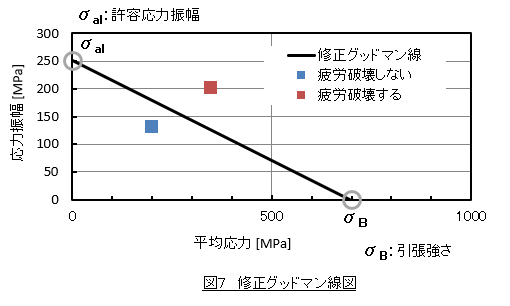
図7において横軸を平均応力,縦軸を応力振幅とします。縦軸切片を許容応力振幅,横軸切片を引張強さとして線を引きます。この線を修正グッドマン線と呼びます。そして応力計算にてあらかじめ平均応力と応力振幅を求めておき,その値をプロットします。プロットが修正グッドマン線の上にあれば疲労破壊すると判定され,下にあると疲労破壊しないと判定します。
おわりに
以上が強度計算の方法です。少し長かったですね。強度計算,疲労破壊でお困りのときは,RTデザインラボにご相談ください。
参考文献
1) 日本機械学会,金属材料 疲労強度の設計資料,Ⅰ,(S63)
2) 石橋,金属の疲労と破壊の防止,養賢堂,(1967)
3) 日本機械学会,機械工学便覧 A4 材料力学,(1992)

